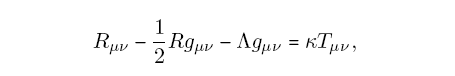1Cosmological constant et dark energy sont deux expressions qui recouvrent des notions intimement liées. Leur emploi n’est toutefois ni totalement équivalent ni exempt d’un certain parti pris dans un débat qui passionne la communauté des cosmologistes et des physiciens des hautes énergies depuis maintenant un peu plus de dix ans1. Dans cette courte note, on se propose de revisiter les grandes étapes qui ont jalonné la brève histoire de la constante cosmologique, de son introduction il y a près d’un siècle à son reniement qui a rapidement suivi, de sa réapparition triomphale sur la scène cosmologique à la fin du xxe siècle au fameux problème cosmologique qu’elle suscite aujourd’hui, pour finir en s’interrogeant, et s’il n’y avait aucun problème avec la constante cosmologique ?
2Lorsqu’Einstein a incorporé la gravitation dans un contexte relativiste, il a été conduit à revoir complètement la conception de l’espace-temps. Celui de la relativité restreinte — l’espace-temps de Minkowski — était déjà considérablement différent de l’espace-temps classique — newtonien — avec l’imbrication du temps et de l’espace en un concept unique et la fin du temps absolu qui s’écoule uniformément, extérieur à toute autre notion. Avec la gravitation relativiste et la théorie de la relativité générale, l’espace-temps se courbe sous l’effet de la matière et de l’énergie, et les équations qui relient la structure de l’espace-temps à son contenu de matière et de rayonnement sont connues sous le nom d’équations de champ d’Einstein [Einstein 1916]. Une étape ultime sera franchie avec la cosmologie relativiste, dont on peut dater les prémices à l’article d’Einstein de 1917 [Einstein 1917]. L’espace-temps était déjà en puissance un concept dynamique dans la relativité générale car sa structure évoluait au gré des distributions d’énergie de l’univers. Il devient degré de liberté dynamique — le facteur d’échelle, a(t) — qui se déploie dans les modèles cosmologiques relativistes.
3Dans son article de 1917, Einstein applique sa jeune théorie de la relativité générale à l’univers dans son ensemble. À l’époque, la notion de galaxie n’a pas encore vu le jour, et on comprend que l’état des connaissances sur l’univers à grande échelle soit trop sommaire pour permettre à l’inventeur de la théorie relativiste de la gravitation de fonder sa cosmologie sur des bases observationnelles fiables. Einstein est ainsi conduit à l’hypothèse d’un univers homogène, isotrope et statique. Si les deux premières hypothèses ont encore cours aujourd’hui et forment la base même du principe cosmologique, la dernière hypothèse sera fatale au modèle développé par Einstein. On s’interroge parfois sur la pertinence de cette troisième hypothèse, car elle est clairement mise en défaut par les observations actuelles, alors que l’isotropie a un support observationnel depuis la découverte en 1964 du fond de rayonnement cosmique (ou CBR pour Cosmic Background Radiation) [Penzias & Wilson 1965]. Replacées dans leur perspective historique, ces trois hypothèses sont cependant également audacieuses, car l’univers observé en 1917 est tout sauf isotrope et homogène. Il est cependant nécessaire d’invoquer des arguments de symétrie très forts pour pallier le manque d’information.
- 2 Ce n’est pas toujours vrai d’ailleurs, puisqu’un champ scalaire peut se coupler à la gravitation p (...)
4Revenons sur l’hypothèse statique. La gravitation est une interaction attractive2. Une conséquence inévitable est que pour compenser les effets de la gravitation afin de rendre l’univers statique, il faut inventer un ingrédient supplémentaire, ce que fait Einstein dans cet article de 1917 avec la constante cosmologique λ (aujourd’hui Λ). Les équations du champ de gravitation prennent alors une forme légèrement modifiée par rapport à celles de 1915, par l’adjonction du terme — Λgμν au premier membre,
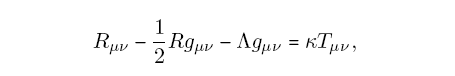
- 3 On notera à ce sujet un modèle d’univers assez pathologique, proposé par K. Gödel [Gödel 1949]. Il (...)
mais leur forme préserve la conservation du tenseur Tμν représentant le contenu matériel, Tμν;μ = 0. La constante cosmologique, placée ici au premier membre des équations d’Einstein, s’oppose aux effets attractifs du champ de gravitation (lorsqu’elle est choisie positive3). Il est notable qu’Einstein ne se soit pas rendu compte que le modèle d’univers statique qu’il venait de proposer souffrait d’un défaut rédhibitoire : il était instable.
- 4 “We have no reason to think that λ is not so small as to be entirely beyond observation. .. I woul (...)
- 5 “For regions of great size, it can be shown that effects could result from a very small value of Λ(...)
- 6 “If one ascribes a small value to the ‘cosmological constant’ Λ, the presence of this term will no (...)
- 7 “Einstein... completely rejected the cosmological term as superflous and no longer justified. I fu (...)
- 8 “I agree with Einstein’s second guessing and think Λ = 0 is most likely.”
5La suite de l’histoire de cette constante cosmologique est connue. Après la découverte de l’expansion de l’univers (Friedmann [Friedmann 1924] et Lemaître [Lemaître 1927] sur la base d’arguments théoriques, Hubble [Hubble 1929] sur celle d’observations astronomiques) et donc l’abandon de l’hypothèse statique, Einstein aurait, dans une lettre à Weyl, regretté d’avoir introduit le terme cosmologique. Les cosmologistes en revanche y étaient attachés, comme Hoyle [Hoyle 1948] ou Bondi et Gold [Bondi & Gold 1948] et leur modèle d’univers en expansion stationnaire, comme Lemaître et son univers hésitant, ou comme Eddington [Eddington 1933] qui observait à juste titre qu’en l’absence de constante cosmologique, il fallait donner à l’univers un âge inférieur à celui de certains des objets (étoiles) qui le constituent pour accommoder les propriétés dynamiques observées aujourd’hui. Malgré ces objections et le soutien des cosmologistes [Eddington 1933, 22]4, [Tolman 1936, 191]5, la constante cosmologique tombe progressivement dans une forme d’oubli, reléguée au rang de curiosité historique. D éminents physiciens, auteurs influents, comme Landau [Landau & Lifshitz 1951, 382] 6 ou Pauli [Pauli 1958, 220]7 et Feynman [Feynman 1995, 149]8 bien plus tard, ne voyaient pas la nécessité de ce terme (selon Ginzburg, « Landau hated the idea of the A term », [Ginzburg 2001, 170]).
6La constante cosmologique réapparaît dans la littérature scientifique au milieu des années 1980 [Peebles 1984], [Turner, Steigman & Lawrence 1984] pour accommoder le modèle FLRW (Friedmann [Friedmann 1924], Lemaître [Lemaître 1927], Robertson [Robertson 1935], Walker [Walker 1937]) aux observations disponibles à l’époque, mais c’est véritablement l’année 1998 qui marque un tournant dans la cosmologie moderne. C est cette année que les premiers résultats des campagnes d’observations des supernovœ IA (SN Ia) sont publiés [Riess 1998], [Perlmutter 1999]. Il s’agit d’objets stellaires extrêmement brillants, donc observables à très grande distance dans l’univers, et dont l’évolution physique est bien comprise, de sorte que ces étoiles qui explosent ont une luminosité absolue connue avec une précision remarquable : ce sont des chandelles. Ces propriétés en ont fait des candidats idéaux pour les campagnes astronomiques d’observations d’objets très éloignés et donc très anciens. Cela permet d’atteindre la dynamique de l’univers en expansion avec une précision jusque là inégalée, repoussant la courbe que Hubble avait produite en son temps à des redshifts inconnus jusqu’alors. Si elle n’est pas une surprise pour les cosmologistes [Krauss & Turner 1995], la nouvelle connaît un retentissement considérable : l’expansion de l’univers s’accélère ! C’est presqu’à un changement de paradigme que l’on assiste. Jusque là, les courbes de luminosité apparente versus redshift (ou distance vs vitesse) étaient caractérisées par des paramètres comme la constante de Hubble H0 ou le paramètre de décélération q0, ainsi dénommé car il devait caractériser un univers en expansion dont le taux d’expansion décroît au cours du temps. Les résultats du Supernova Cosmology Project et du High-Z supernovae search team en 1998, confirmés et affinés depuis, ont montré que le paramètre de décélération mesuré aujourd hui est négatif. Premier candidat à être cause de l’accélération observée, la constante cosmologique fait un retour triomphal dans la littérature scientifique. Cette même année apparaît cependant, introduit par Huterer et Turner [Huterer & Turner 1999], le terme d’énergie sombre (dark energy) pour décrire une série de concepts alternatifs à la constante cosmologique. Probablement influencés par les travaux du début des années 1980 sur l’inflation, ces concepts alternatifs reposent sur l’observation que les théories des champs se couplent facilement à la gravitation de manière répulsive et sont donc à même de produire une accélération de l’expansion cosmique. L’intrusion des théories des champs (la physique des particules élémentaires) en cosmologie remonte à Pauli, lorsqu’il a observé que le terme de constante cosmologique avait la structure de l’énergie du vide dans les théories quantiques des champs, Tμν = ρΛc2ημν (si ρΛ = –ρΛc2) dans le référentiel comobile, ημν étant la métrique de Minkowski. De nombreuses difficultés sont liées à cette observation, car la valeur mesurée pour la constante cosmologique (ou pour la densité d’énergie qui lui est associée) est sans aucune mesure avec la valeur attendue lorsqu’elle est interprétée comme une énergie du vide. On assiste à un désaccord monumental (la première valeur est typiquement 10120 fois plus petite que la seconde), connu sous l’euphémisme de problème de la constante cosmologique. Une fois cette difficulté admise, la notion de constante cosmologique telle qu’introduite par Einstein est remise en question et l’on cherche à élaborer des modèles cosmologiques alternatifs.
7Pour bien comprendre la diversité des pistes explorées pour rendre compte de l’accélération de l’expansion de l’univers, il est bon de repréciser les éléments essentiels qui fondent un modèle cosmologique. On entend par cosmologie le fait d’appliquer une théorie de la gravitation à une échelle suffisante pour pouvoir idéaliser le contenu de l’univers et le représenter par un “fluide cosmique” dont les propriétés, couplées à la gravitation, déterminent la géométrie de cet univers. Un tel modèle suppose de travailler à très grande échelle, typiquement 1024 – 1026m. Il suppose également une théorie de la gravitation, c’est-à-dire essentiellement une géométrie Gμν dans les théories métriques. Il suppose encore des données (sinon des hypothèses) sur le contenu matériel et énergétique de l’univers, c’est-à-dire la forme du tenseur Tμν. Il suppose enfin des hypothèses de symétrie qui contraignent le tenseur métrique gμν de manière à permettre d’exprimer à la fois Gμν et Tμν.
8Le modèle cosmologique standard est fondé sur le principe cosmologique qui suppose un espace-temps homogène et isotrope et restreint la métrique à celle proposée par Friedmann, Robertson et Walker,
avec σ = r/a(t) la coordonnée comobile et a(t) le facteur d’échelle de l’univers, k = 0, ±1 sa courbure. En dehors du paramètre k, la dynamique d’un univers obéissant au principe cosmologique repose sur le seul degré de liberté de cette métrique, le facteur d’échelle a(t). La théorie de la gravitation appliquée dans ce modèle est celle d’Einstein, appelée aussi relativité générale et dont il a été question plus haut, soit
où le tenseur de Ricci Rμν comprend des dérivées premières et secondes des gμν. Enfin, pour ce qui concerne le contenu matériel de l’univers, il s’agit d’un “fluide cosmique”
avec diverses composantes w obéissant à des équations d’état de la forme
Avec l’ensemble de ces ingrédients, la dynamique de l’univers, régie par les équations d’Einstein,
conduit aux équations de Friedmann, équations différentielles pour le facteur d’échelle a(t). Ce qui valide l’utilisation de la relativité générale comme théorie de la gravitation dans l’esprit du modèle cosmologique standard, c’est la capacité de la relativité générale à décrire l’ensemble des phénomènes gravitationnels à des échelles ordinaires, notamment ses succès dans les trois tests classiques à l’échelle du système solaire.
9On effectue ensuite un inventaire des composants essentiels de l’univers sur la base des observations accessibles, pour répertorier les diverses formes de matière-énergie. Pour rendre le modèle compatible avec les mesures, on distingue essentiellement trois composantes, la matière froide pM = 0, le rayonnement pR = ⅓(ρRc2) et la constante cosmologique pΛ = —ρΛc2. Notons que le point de vue adopté ici consiste à placer le terme de constante cosmologique au second membre des équations d’Einstein et à le traiter comme un fluide cosmique de densité ρΛ = Λc2/8πG.
- 9 Notons que les cosmologistes ont envisagé bien d’autres formes d’énergie. Mentionnons à côté du ra (...)
10Les mesures les plus significatives sont issues de trois types de campagnes d’observations : celles qui sont basées sur les supernovœ de type Ia déjà évoquées, celles qui analysent les fluctuations du fonds diffus cosmologique, et enfin celles qui se penchent sur les distributions de matière à très grande échelle. Ces observations sont convergentes et conduisent à une proportion très importante de formes de matière-énergie (dite sombre) qui sont encore très mal connues à l’heure actuelle, mais dont la présence est indispensable dans le cadre du modèle cosmologique standard pour expliquer les paramètres cinématiques (constante de Hubble, paramètre de décélération, ...) observés9.
11Parmi les alternatives au modèle cosmologique standard, on peut essentiellement répertorier trois voies d’investigation (pour une classification plus fine, on pourra se reporter à Nobbenhuis [Nobbenhuis 2004, 2006] et pour un exposé détaillé des aspects scientifiques, à Amendola et Tsujikawa [Amendola & Tsujikawa 2010]).
- 10 L’inflation est une phase d’expansion exponentielle de l’univers qui a régi la dynamique dans la p (...)
- 11 Le champ ϕ est ici supposé homogène et ϕ représente la dérivée temporelle.
12Une première piste, évoquée plus haut, consiste à chercher de nouvelles formes d’énergie-matière (d’où le terme de dark energy) qui puissent rendre compte de l’accélération de l’expansion, tout en conservant la relativité générale comme théorie de la gravitation. La quintessence est probablement la plus populaire des théories explorées dans cette direction. Il s’agit d’un champ scalaire ℒmat = ½(gμνδμϕδνϕ–V(ϕ)) soumis à un potentiel V(ϕ) dans l’approximation de roulement lent, c’est-à-dire que comme dans le cas de la phase d’inflation10, l’énergie potentielle très plate domine largement l’énergie cinétique, permettant un couplage répulsif à la gravitation, avec une équation d’état de la forme11

La terminologie, quintessence, évoque la cinquième force et serait associée à une interaction répulsive à très grande distance, portée par une particule de masse exceptionnellement petite à l’échelle des particules élémentaires connues.
13Une autre voie prometteuse également consiste à modifier la théorie de la gravitation sur laquelle est fondé le modèle cosmologique. Rappelons que la relativité générale se déduit de l’action d’Einstein-Hilbert (en l’absence de matière-énergie),
de sorte que par variation de l’action,
entraîne Gμν = 0. La relativité générale, basée sur l’action Seh, est la plus simple des théories métriques de la gravitation. De nombreuses généralisations en ont été proposées, telles que les théories f(R)
ou celles qui incluent davantage de champs, comme la théorie scalaire-tenseur de Brans et Dicke
pour ne citer que ces deux exemples.
14Une solution probablement moins étudiée et pourtant très simple et économique consiste à contourner le principe cosmologique, sans remettre en question ni la théorie de la gravitatioon, ni le contenu ordinaire de matière-énergie. Il s’agit de supposer que notre univers observable est dans une zone où la densité de matière et d’énergie est plus faible qu’en moyenne dans l’univers, de sorte que la gravitation y est localement moins élevée, expliquant en même temps le fort éloignement des SN Ia [Tomita 2001].
15D’autres théories sont susceptibles d’apporter des éléments de solution, comme les axions, particules qui se couplent aux photons et peuvent ainsi expliquer une atténuation de la luminosité apparente des SN Ia plus importante que celle attendue, mais ces approches se heurtent à des difficultés pour l’interprétation des résultats d’observations du CBR ou des grandes structures.
16Le modèle cosmologique standard souffre d’un grand nombre de défauts, communément appelés les problèmes cosmologiques, comme le problème de la constante cosmologique, de la matière noire, de l’horizon, des eliques, des coïncidences, etc. La résolution de ces problèmes passe par des théories ingénieuses, mais hautement spéculatives comme l’inflation, par l’espoir que des campagnes d’observations futures mettront en évidence de nouvelles formes de matière comme les WIMPS (weakly interacting massive particles) ou d’énergie comme la quintessence, ou pourquoi pas, par une remise en question des fondements comme la gravitation ou le principe cosmologique.
17Le problème de la constante cosmologique apparaît clairement comme une source d’inventivité, et c’est peut-être là sa plus grande richesse : la fécondité ! Il est clair que l’énergie du vide n’est pas une piste acceptable, puisque sa valeur est beaucoup trop importante pour produire l’accélération observée. Cela soulève une seconde difficulté, puisqu’il faut trouver une explication à cette valeur trop élevée.
18Et si le mot de la fin revenait à la constante cosmologique [Bianchi & Rovelli 2010], [Bianchi & Rovelli 2010a] ? A pourrait être une constante fondamentale de la physique dont la nature a fixé la valeur, et s’il persiste un désaccord avec les théories quantiques des champs, peut-être est-il dû à une connaissance encore trop imparfaite de ces dernières !